V prvom rade je moja práca tesne spätá s pravidelným rozdelením roviny. Všetky obrazy za posledných niekoľko rokov z toho vychádzajú, z princípu kongruentných figúr, ktoré, bez toho aby zanechávali „prázdne miesta“, donekonečna, alebo aspoň akoby bez ohraničenia zapĺňajú rovinu. Ako to raz váš otec bezchybne vyjadril: pre mňa je to vždy otázka toho, ako neohraničenú plochu ohraničiť, ako ju „ukončiť“, urobiť z nej „kompozíciu“. Musím bojovať, dalo by sa povedať, s dvomi rozdielnymi potiažami, ktoré spoločne činia celú túto záležitosť tak okúzľujúcu: za prvé „nájdenie“ alebo uhádnutie či poskladanie dohromady indetických figúr, ktoré potrebujem; za druhé poskladanie uzavretej roviny so špecifickými rozmermi, v ktorej tieto figúry, ktoré v sebe takpovediac nesú nekonečnosť či nespútanosť, ležia spútané a uväznené.
Táto dvojitá báza mojich obrazov je teda abstraktná. Motivácia mojich pokusov nemá čo do činenia s naozajstnou realitou
M.C. Escher – Dopis synovcovi Rudolfovi Escherovi, 17.1.1944
V roku 1922 navštívil Escher palác Alhambra v španielskej Granade. Maurské ornamenty tvoriace mozaiky na stenách a dlažbe ho nadchli natoľko, že sa začal zaujímať o to, ako pravidelne rozdeliť rovinu. Jeho prvým dielom s využitím pravidelného rozdelenia roviny je drevorez Osem hláv z roku 1922
Zanedlho však na pár rokov snahy o delenie plochy zanechal, nakoľko nebol spokojný ani s tým, koľko času mu to zaberalo, ani so svojimi výsledkami.
S rastúcim napätím Mussoliniho režimu sa v tridsiatompiatom roku odsťahoval Escher so svojou rodinou do Švajčiarska. Pre nedostatok inšpirácie z okolitej krajiny sa rozhodol pre ďalši výlet do stredomoria. Druhýkrát navštívil Alhambru v roku 1936. Znova podľahol čaru maurských obrazcov. Zanietene sa snaží objavovať rád v symetrických vzoroch, ktorými by mohol pokryť nekonečnú plochu. Sám to považuje za fascinujúcu hru, či hobby. Vďaka svojmu bratovi Berendovi, ktorý bol geológom a rozpoznal matematické princípy v jeho kresbách, sa zoznamuje s textami Georgyho Pólya a teóriou kryštalografických grúp.
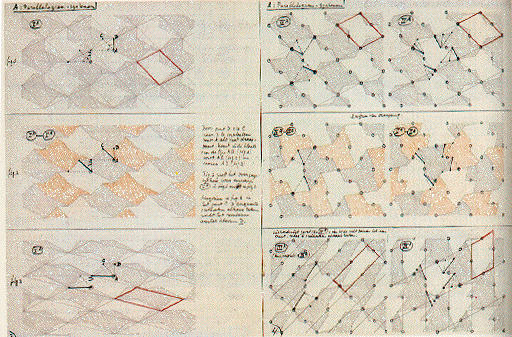
Rovnobežníkové systémy
Kosoštvorcové systémy
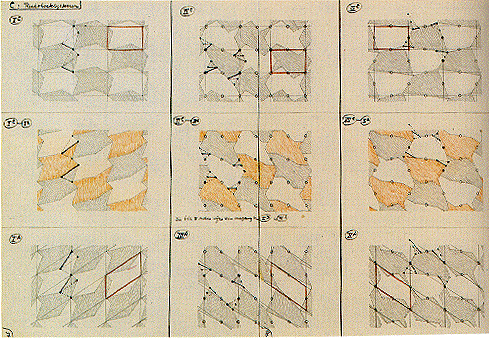
Obdĺžnikové systémy
Tapetové grupy
Kryštalografické grupy boli prvýkrát popísané roku 1891 ruským matematikom Yevgrafom Stepanovichom Fyodorovom.
Tapetová grupa je planárna kryštalografická grupa – grupa izometrií dvojrozmerného euklidovského priestoru obsahujúca dve lineárne nezávislé translácie. Existuje 17 tapetových grúp.
Základnými oblasťami rozdelenia plochy sú: kosodĺžnik, kosoštvorec, obdĺžnik, štvorec, šesťuholník.
Izometria (zhodnosť) dvojrozmerného euklidovského priestoru je bijekcia tohto priestoru na seba zachovávajúca vzdialenosti:
Priame:
1.Identita
2. Translácia
3. Rotácia
Nepriame:
4. Osová súmernosť
5. Posunutá osová súmernosť
Izometrie vytvárajú symetrie vo vnútri základnej oblasti (uvažujeme len rotácie o 2π, π, 2π/3, π/2, π/3).
Escherovi sa podarilo zobraziť 15 tapetových grúp. Napriek tomu, že ho pravidelné delenie plochy fascinovalo a pohlcovalo, používal ho vo svojom diele len ako nástroj, nie ako výsledný obraz.
Klasifikácia tapetových grúp na Escherových rozdeleniach roviny
Používame klasické kryštalografické značenie:
písmená p a c – bližšie určujú základnú oblasť
číslo n – udáva rád rotácie vo vzore (rotáciu o 2π/n)
písmená m a g – môžu nasledovať za číslom n ak tapeta obsahuje osovú súmernosť (m), alebo posunutú osovú súmernosť (g)
v obrázkoch je nasledovné značenie:
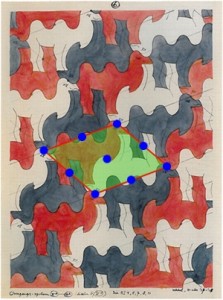
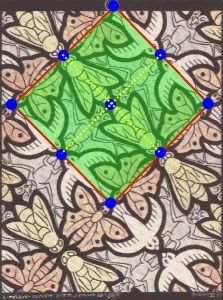
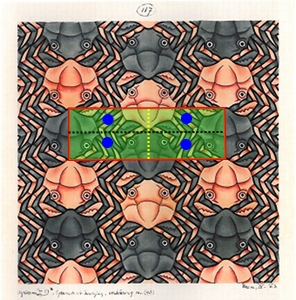
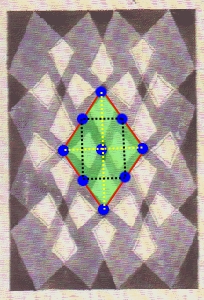
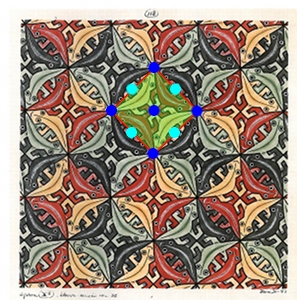
červená farba ohraničuje základnú oblasť (jednu dlaždicu)
žltá bodkovaná čiara označuje os osovej súmernosti
čierna bodkovaná čiara označuje os posunutej súmernosti
modrý bod – stred rotácie o π
bledomodrý bod – stred rotácie o π/2
purpurový bod – stred rotácie o π/3
bordový bod – stred rotácie o π/6
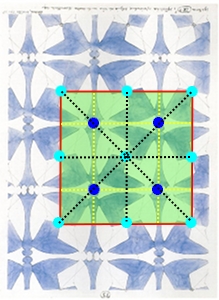
p1
Najjednoduchšia tapetová grupa. Pozostáva z dvoch translácií o vektory tvoriace základnú oblasť. Vnútri oblasti je identita.
Základnou oblasťou je rovnobežník.
p2
Grupa obsahujúca rotáciu rádu 2. Stred otáčania je stred rovnobežníka, ktorý tvorí základnú oblasť.
pm
Grupa obsahuje osovú súmernosť. Smer osi je rovnaký ako smer jedného translačného vektoru a kolmý k smeru druhého translačného vektoru.
Základná oblasť je obdĺžnik.
pg
Grupa obsahuje posunutú osovú súmernosť s osou v smere jedného translačného vektoru a kolmou k smeru druhého translačného vektoru.
Základnou oblasťou je obdĺžnik.
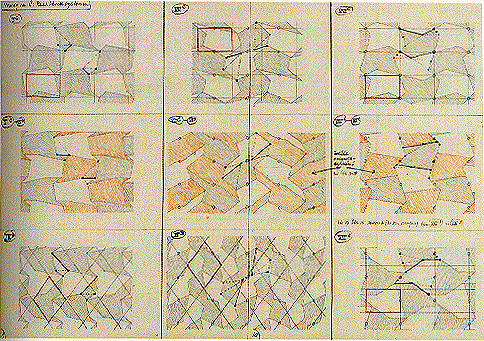
pmm
Grupa obsahujúca dve osové súmernosti kolmé k translačným vektorom. V priesečníku osí je stred rotácie 2. rádu a preto môžeme grupu označiť aj ako p2m.
Základná oblasť je obdĺžnik.
pgg
V tejto grupe sú dve posunuté osové súmernosti s osami kolmými k translačným vektorom. Rovnako obsahuje aj rotácie 2, rádu, so stredmi neležiacimi na osiach.
Základná oblasť je obdĺžnik
pmg
Grupa obsahujúca posunutú osovú súmernosť a osovú súmernosť, ktorých osi sú kolmé k translačným vektorom. Obsahuje aj rotácie 2. rádu.
Základná plocha je obdĺžnik
cm
Grupa cm je tvorená osovou súmernosťou v kosoštvorcovej základnej oblasti. Os súmernosti rozpoľuje uhol translačných vektorov. V tejto grupe existuje aj posunutá osová súmernosť s osou rovnobežnou s osou súmernosti. Grupa pm sa dá nájsť na rovnakom vzore, rozdiel je v menšej základnej oblasti u grupy cm.
cmm
Základnou oblasťou tejto grupy je kosoštvorec, ktorého uhlopriečky sú osami dvoch osových súmerností. Priesečník osí je stred rotácií 2. rádu. Nachádzajú sa tu aj posunuté osové súmernosti.
p4
Grupa p4 je generovaná rotáciami o π/2 a neobsahuje ani osovú, ani posunutú osovú súmernosť. Obsahuje aj rotácie 2. stupňa, stredy sú vyznačené bledomodrou farbou.
Jej základná oblasť je štvorec.
p4m
M.C. Escher tento vzor vo svojom diele nepoužil.
Táto grupa obsahuje rotácie stupňa 4 a taktiež stupňa 2. Zároveň obshuje osové súmernosti tvorené 4 osami prechádzajúcimi stredmi otáčania a zvierajúcimi medzi sebou uhol π/4.
p4g
Grupa obsahuje rotácie 4. rádu, taktiež rotácie 2. rádu. Osi súmernosti prechádzajú stredmi otáčania rotácií 2. rádu a neprechádzajú stredmi rotácií 4. rádu. V tejto grupe existujú posunuté osové súmernosti s osami v 4 smeroch generovaných stredmi otáčaní.
Základnou oblasťou je štvorec.
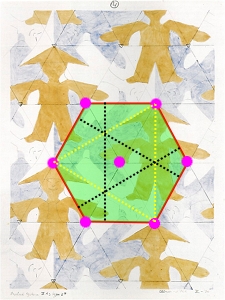
p3
Grupa obsahuje len rotácie rádu 3.
Základnou oblasťou je šesťuholník.
p31m
Táto grupa má tiež rotácie o 120˚. Nachádzajú sa v nej aj osové súmernosti, ktorých osi zvierajú uhol 60˚. Obsahujú taktiež posunuté osové súmernosti.
Základnou oblasťou je šesťuholník.
p3m1
Grupa obsahuje rovnako ako p31m rotácie stupňa 3 a osové súmernosti, s osami zvierajúcimi 60˚. Osi v tomto prípade prechádzajú strredmi rotácií. Obsahuje aj posunuté osové súmernosti.
Základná oblasť je šesťuholník.
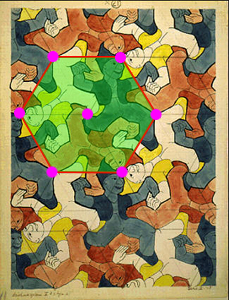
p6
Grupa p6 je najjednoduchšia grupa obsahujúca otáčanie 6. rádu. Obsahuje aj otáčania rádu 2 a 3.
Základná plocha je šesťuholník.
p6m
Esher túto grupu nazobrazil.
Grupa p6m obsahuje rovnako ako p6 rotácie o 60˚, 120˚ a 180˚ . Navyše obsahuje aj osové súmernosti, pričom osi prechádzajú všetkými stredmi rotácií.
Základnou oblasťou je šesťuholník.
Za zmienku stojí, že v trojrozmernom priestore je 230 kryštalografických grúp a v štvorrozmernom 4783^(18)
Escher sa zaoberal vo svojich obrazoch aj zafarbením jednotlivých motívov. V tejto oblasti predbehol matematický výskum. Dá sa povedať, že vo svojich náčrtoch popísal takmer všetky rovinné symetrie obsahujúce 2, 3, 4 alebo 6 farieb a výrazne tak prispel k teórii polychromatických (viacfarebných) grup.
Rovnomerné rozdelenie plochy podobnými vzormi
Escher išiel ešte ďalej a pokúsil sa pridať do rozdelenia roviny prvok podobnosti.
Podarilo sa mu to napriklad v obraze Menší a menší z roku 1956. Jašter sa smerom od okrajov k stredu postupne zmenšuje.
Taktiež sa M.C. Escherovi podarilo zobraziť neperiodické rozdelenie roviny. Je to rozdelenie, v ktorom nepoužívame transláciu.
Ako bolo vyššie spomenuté, Escher delenie plochy používal ako nástroj pre svoje obrazy. Svoje majstrovstvo geometrie pravidelných útvarov preukázal naplno v diele Metamorfózy, ktoré postupom svojho života dopĺňal. Prelína tu jednotlivé delenia plochy medzi sebou a na konci sa dostáva k prvému vzoru. Pre jeho najznámejšie diela je takéto vyjadrenie nekonečna typické.
