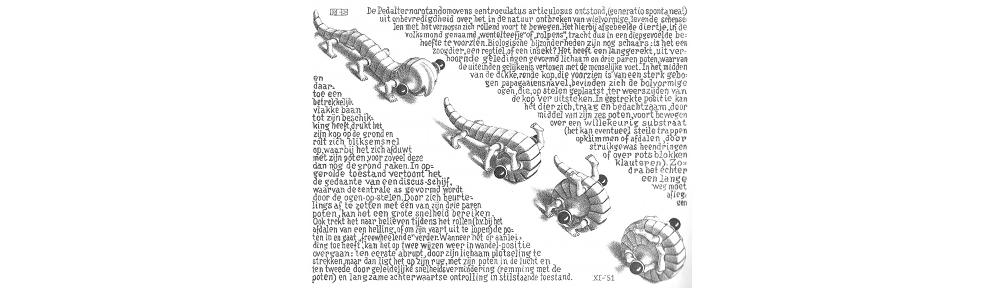
V roku 1954 sa Escher stretol s geometrom H. S. M. Coxeterom, ktorý mal výrazný vplyv na jeho ďalšiu tvorbu. V roku 1958 napísal Coxeter článok o symetriách, v ktorom sám zobrazil dláždenie na Poincarého kruhovom modeli hyperbolickej geometrie. Tento článok poslal Escherovi, ktorý bol fascinovaný, nakoľko mu to ukázalo, ako vytvoriť nekonečný vzor v kruhu.

Poincarého kruhový model

Model je vytvorený kruhom, kde všetky body vnútri kruhu, neležiace na hraničnej kružnici sú bodmi hyperbolickej roviny. Prieniky kruhu a kružníc kolmých na hraničnú kružnicu (ich dotyčnice zvierajú pravý uhol), spolu s priemermi hraničnej kružnice nazývame priamkami hyperbolickej roviny.

Osovou súmernosťou v Poincarého modeli rozumieme:

Ak je os priemerom hraničnej kružnice, potom je to osová súmernosť v euklidovskej rovine.

Ak os nie je priemerom hraničnej kružnice, potom je to kruhová inverzia v euklidovskej rovine podľa kružnice reprezentujúcej priamku v hyperbolickej rovine.

Skladaním osových súmerností vygenerujeme všetky súmernosti v hyperbolickej rovine.

Kruhová limita I vznikla krátko po tom, ako umelec obdržal Coxeterov článok.

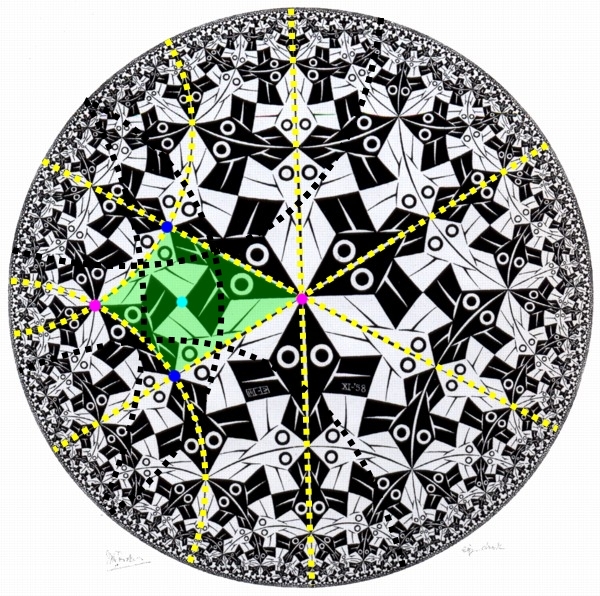V obraze Kruhová limita III sa Escherovi nepodarilo vytvoriť dláždenie Poincarého modelu i keď to tak na prvý pohľad nevyzerá. Chrbty rýb však tvoria  priamky zvierajúce s hraničnou kružnicou uhol presne 80˚.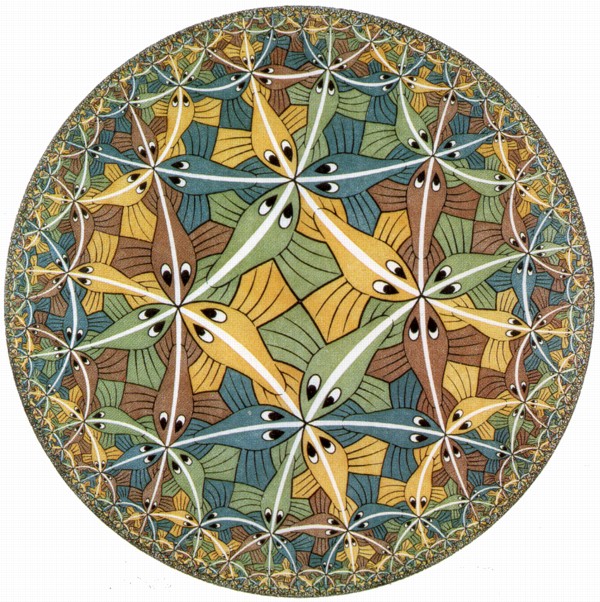

Ubíja ma to, najprv konečne dokončiť tú litografiu a potom sa štyri dni so zaťatými zubami snažiť o deväť dobrých sútlačí tých nanajvýš zložitých kruhových hraníc vo farbe. Každý z výtlačkov vyžaduje dvadsať otlačkov: päť stočiek, každú z nich vytlačiť štyrikrát. A to všetko s tým zvláštnym pocitom, že každá z tých vecí je mílnikom v mojom vývoji a že okrem mňa nikdy nebude nikto iný, kto by to realizoval.

Dopis synovi Arthurovi, 20.3.1960

Celkovo vytvoril Escher 4 kruhové limity. V 70tych rokoch sa matematikovi Douglasovi Dunhamovi podarilo vynájsť algoritmus s využitím Hamiltonovských kružníc na kreslenie hyperbolického dláždenia.

Escherova Kruhová limita IV – Nebo a peklo